Publishing Screenshots, Markdown Documents, and Other Files on DigitalOcean Spaces

A couple of weeks ago at DigitalOcean, we introduced Spaces—beautifully simple and reliable object storage. With Spaces, you can host and serve static files without having to worry about security, scaling, disk space, and all the fun things that come with maintaining a server.

Spaces is compatible with the S3 API. This is important because it makes Spaces fully available to use with a huge number of applications and tools right away. In this post, I'll talk about how I'm using Dropshare to share screenshots, markdown files (rendered as HTML!), and all sorts of files on a custom domain name backed by Spaces.

Features

The most important part about this is that you are able to use your own domain name instead of bucket.region.digitaloceanspaces.com. But that's not all. In addition to simply serving static files, kmlnsr.me also renders markdown files as HTML, with the ability to view the raw Markdown source code. Take a look at this file for example. It's a Markdown file that is rendered as HTML with styling, on the fly. You can view the original Markdown code by appending /raw to the URL. Spaces does not support that natively, though. More on how that works in a bit.

Setup

Uploading files

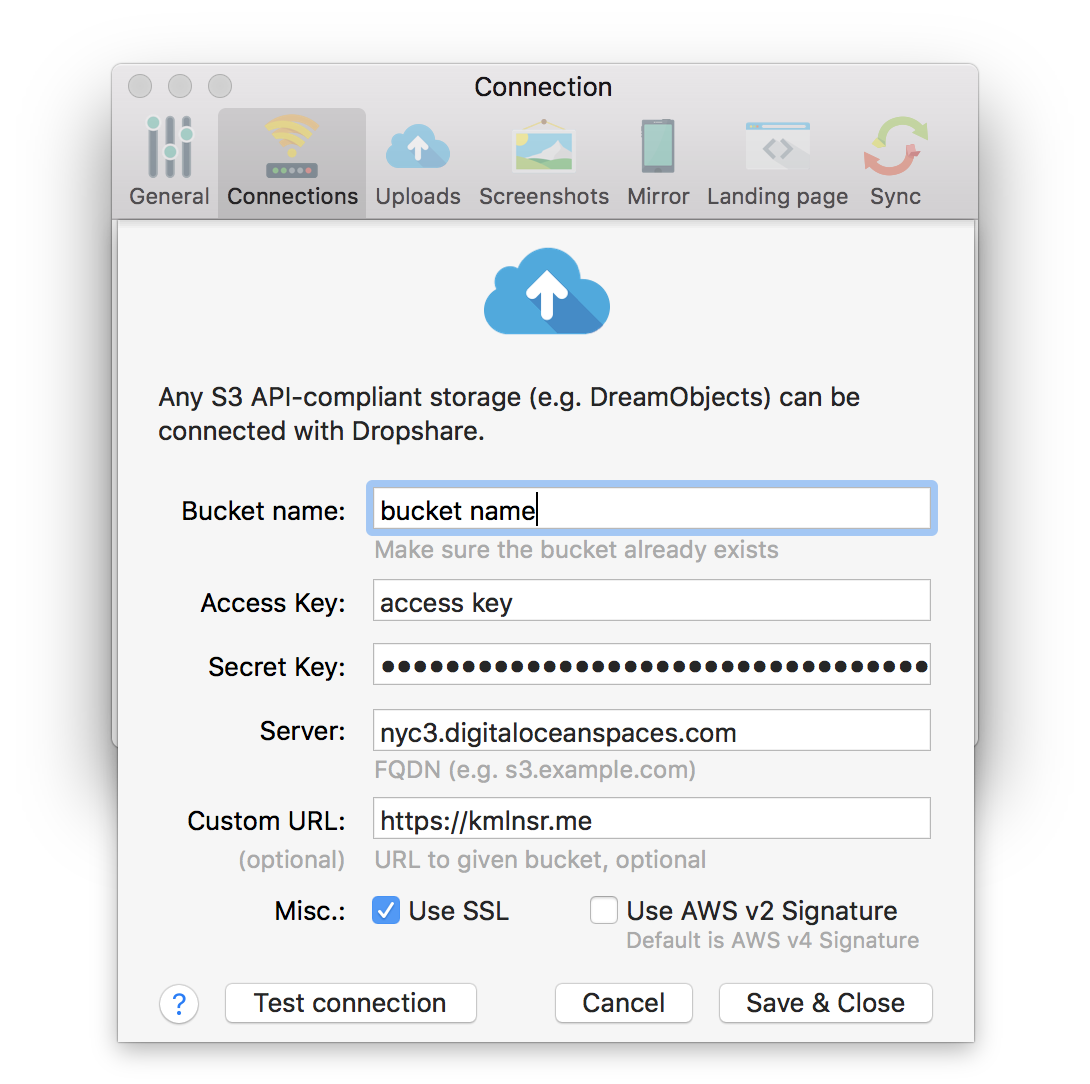
Dropshare uses the S3 API to upload files to Spaces. It supports custom S3 endpoints natively, so it's very easy to configure. Simply create a new connection with the following configuration:

You might also want to replace the default screenshot hotkey to use Dropshare. First, disable the default hotkey in System Preferences→Keyboard→Shortcuts→Screen Shots. Then, configure Dropshare to use that shortcut in the Screenshots tab.

For reference, here's Dropshare documentation on setting up DigitalOcean Spaces connections:

• How to set up a DigitalOcean Spaces connection with Dropshare

Serving files

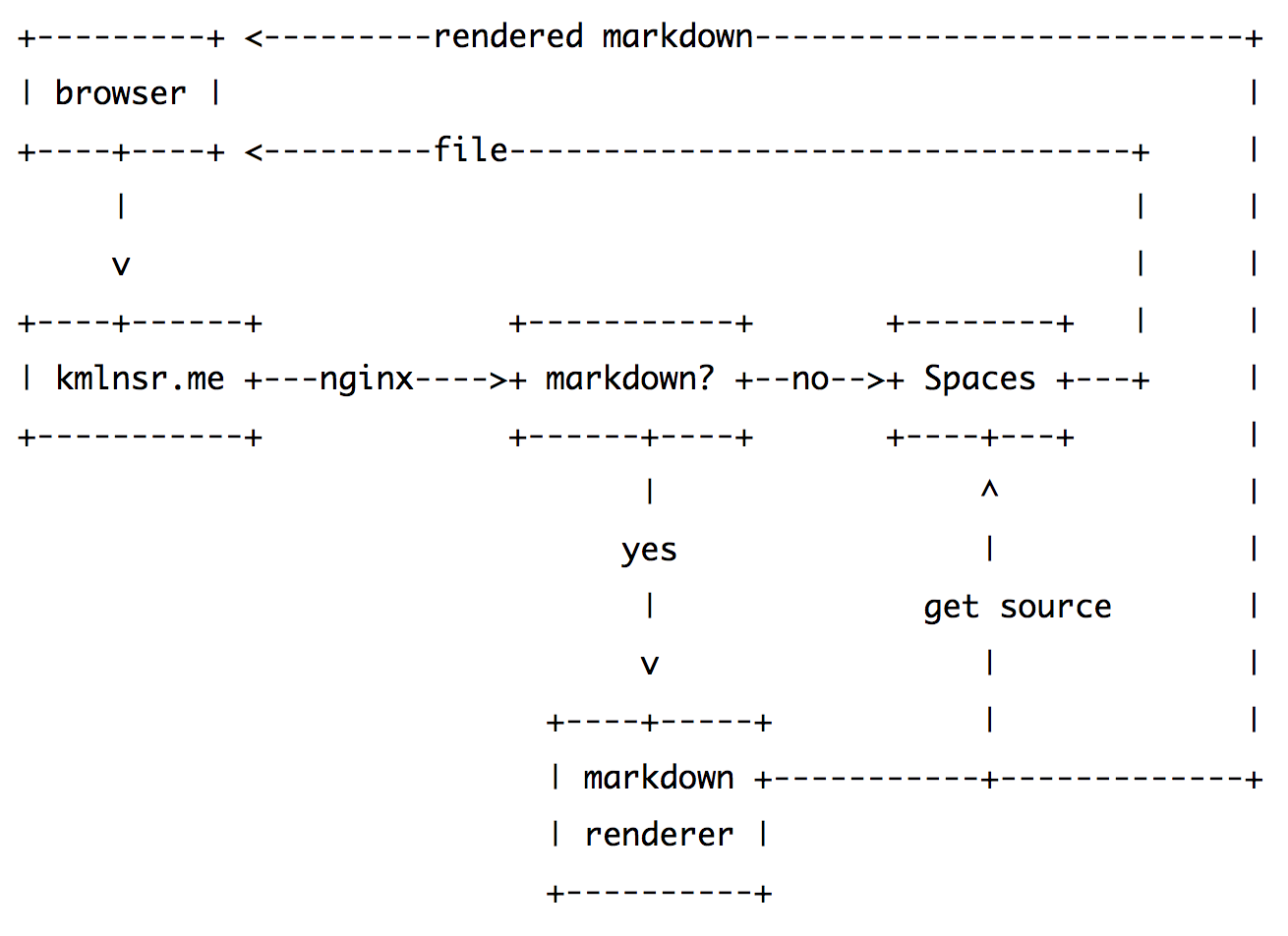
Now this diagram is a bit more complex than the previous one, so let's break it down piece by piece.

1. A browser makes a request to a file on kmlnsr.me (like the screenshot above!). The request goes to a Droplet with nginx running on it.

2. Nginx looks at the URL and checks if it is a Markdown file.

   a. If it is not a Markdown file, it proxies the request to Spaces, fetching the file and serving it as is to the browser.

   b. If it is a Markdown file, it fetches the file from Spaces, passes it to a markdown renderer, and then serves the HTML version to the browser.

Nginx Configuration

Let's build the configuration bit by bit, starting with a basic one:

server {
    listen 80;

    server_name kmlnsr.me;
    root /dev/null;
    
    location = / {
        return 302 https://kamal.io;
    }
}

Right now, it doesn't do much. http://kmlnsr.me/ redirects to https://kamal.io, and everything else returns a 404 Not Found error.

Serving static files

The idea behind serving static files is fairly simple. Proxy requests to https://kmlnsr.nyc3.digitaloceanspaces.com without any post-processing.

Because we will set up a couple of location blocks, let's extract the common directives into their own file that we can simply include wherever we need it. I saved it in /etc/nginx/snippets/spaces_proxy.conf.

proxy_http_version     1.1;
proxy_set_header       Authorization '';
proxy_hide_header      x-amz-id-2;
proxy_hide_header      x-amz-request-id;
proxy_hide_header      Set-Cookie;
proxy_ignore_headers   "Set-Cookie";
proxy_intercept_errors on;

Now, let's serve some static files! location / matches all requests—except / itself as it is matched by a previous location block.

location / {
    include snippets/spaces_proxy.conf;
    
    proxy_set_header Host kmlnsr.nyc3.digitaloceanspaces.com;
    proxy_pass https://kmlnsr.nyc3.digitaloceanspaces.com;
}

The proxy_set_header directive is important. Without it, Spaces would receive kmlnsr.me as the Host and wouldn't know what bucket it is, as it doesn't understand custom domain names.

With this config, everything should work as if you are accessing https://YOUR_SPACE.nyc3.digitaloceanspaces.com directly.

Serving Markdown files

There are two parts to this feature:

1. Serving the raw Markdown file as-is
2. Taking that, rendering it, and serving it as HTML

Serving raw Markdown

Right now, if you browse to /markdown_file.md/raw, you would get a 404 Not Found error. This is expected, because you are trying to access a file named raw in the directory /markdown_file.md.

In order to fix that, we need to modify the URL that is passed to Spaces, removing the /raw bit. This can easily be done with a bit of RegEx magic.

location ~ ^/(.*)\.md/raw$ {
    include snippets/spaces_proxy.conf;
    
    add_header Content-Type text/plain;
    proxy_set_header Host kmlnsr.nyc3.digitaloceanspaces.com;
    proxy_pass https://kmlnsr.nyc3.digitaloceanspaces.com/$1.md;
}

The URI pattern ^/(.*)\.md/raw$ matches requests in the format of */markdown_file.md/raw, capturing the path to the Markdown file in the process. Once we have that, we simply set the URL that is sent to Spaces to */markdown_file.md.

This way, we get the file's content, and serve it back to the browser. Setting the Content-Type header to text/plain asks browsers to display the file as plain text instead of downloading it.

Rendering Markdown as beautiful HTML

I've had this set up for years, so it uses a simple PHP script to do the hard work. You can download the source code here, hosted on Spaces of course :)

In that archive, you will find two files:

1. markdown.php this is the Markdown library that I'm using. It's a very old version, but it has been working well so why bother replacing it ¯\_(ツ)_/¯
2. md.php this is the file that Nginx runs. It's not super complex, but it basically requests the source (using the /raw URL), parses it using the Markdown library, and serves it along with a basic CSS stylesheet. Unfortunately, I don't remember where I got the stylesheet from.

You will need to adjust a couple of things in md.php. First, set the $url variable (line 5) to your own hostname. Then, copy the stylesheet to your Space and update the URL on line 21.

location ~ \.md$ {
    fastcgi_pass    unix:/var/run/php5-fpm.sock;
    fastcgi_param   DOCUMENT_ROOT    $document_root;
    fastcgi_param   SCRIPT_NAME      $uri;
    fastcgi_param   SCRIPT_FILENAME  /srv/markdown/md.php;
    include fastcgi_params;
}

This is a basic php-fpm configuration. The most important part is that SCRIPT_FILENAME is fixed and always set to the md.php handler.

Putting it all together

Once you're all done, the config file will look like this:

server {
    listen 80;

    server_name kmlnsr.me;
    root /dev/null;
    
    location = / {
        return 302 https://kamal.io;
    }
    
    location / {
        include snippets/spaces_proxy.conf;
    
        proxy_set_header Host kmlnsr.nyc3.digitaloceanspaces.com;
        proxy_pass https://kmlnsr.nyc3.digitaloceanspaces.com;
    }

    location ~ ^/(.*)\.md/raw$ {
        include snippets/spaces_proxy.conf;
    
        add_header Content-Type text/plain;
        proxy_set_header Host kmlnsr.nyc3.digitaloceanspaces.com;
        proxy_pass https://kmlnsr.nyc3.digitaloceanspaces.com/$1.md;
    }

    location ~ \.md$ {
        fastcgi_pass    unix:/var/run/php5-fpm.sock;
        fastcgi_param   DOCUMENT_ROOT    $document_root;
        fastcgi_param   SCRIPT_NAME      $uri;
        fastcgi_param   SCRIPT_FILENAME  /srv/markdown/md.php;
        include fastcgi_params;
    }
}

That's all there is to it! Reload Nginx and you should be all set.

Optional improvements

Nicer error pages

Check this out. Who wouldn't want that over this?! Luckily, this is super easy to set up. All you need to do is add the following to your server block.

proxy_intercept_errors on;
error_page 403 /404.html;
error_page 404 /404.html;
location = /404.html {
    root /srv/www;
}

Finally, put whatever 404 page you want in /srv/www/404.html and Nginx will serve it whenever a 404 or 403 error occurrs, which S3-compatible endpoints tend to send when files are not found.

Caching

You will probably want to set up some kind of caching in order to reduce latency. Add the following to /etc/nginx/nginx.conf:

proxy_cache_path /srv/www/spaces/cache  levels=1:2    keys_zone=SPACES:50m         inactive=168h  max_size=10g;

You can set the path to whatever you want, of course. Just make sure that www-data has write access to it.

Then, like we did with the common S3 directives, save the following in /etc/nginx/snippets/spaces_cache.conf.

add_header X-Cache-Status $upstream_cache_status;
proxy_cache SPACES;
proxy_cache_valid 1d;
proxy_cache_use_stale error timeout invalid_header updating http_500 http_502 http_503 http_504;

This will cache files for one day. Because every file has a random string appended to it, I don't really worry about the cache period being that long, but you might want to lower it.

Now, go back to your server block, and add the following to every block that has a proxy_pass directive to Spaces.

include snippets/spaces_cache.conf;

SSL

Ok, this is not so optional really. Please set up SSL. With Let's Encrypt, you really have no excuse not to do so.

• How To Secure Nginx with Let's Encrypt on Ubuntu 16.04.

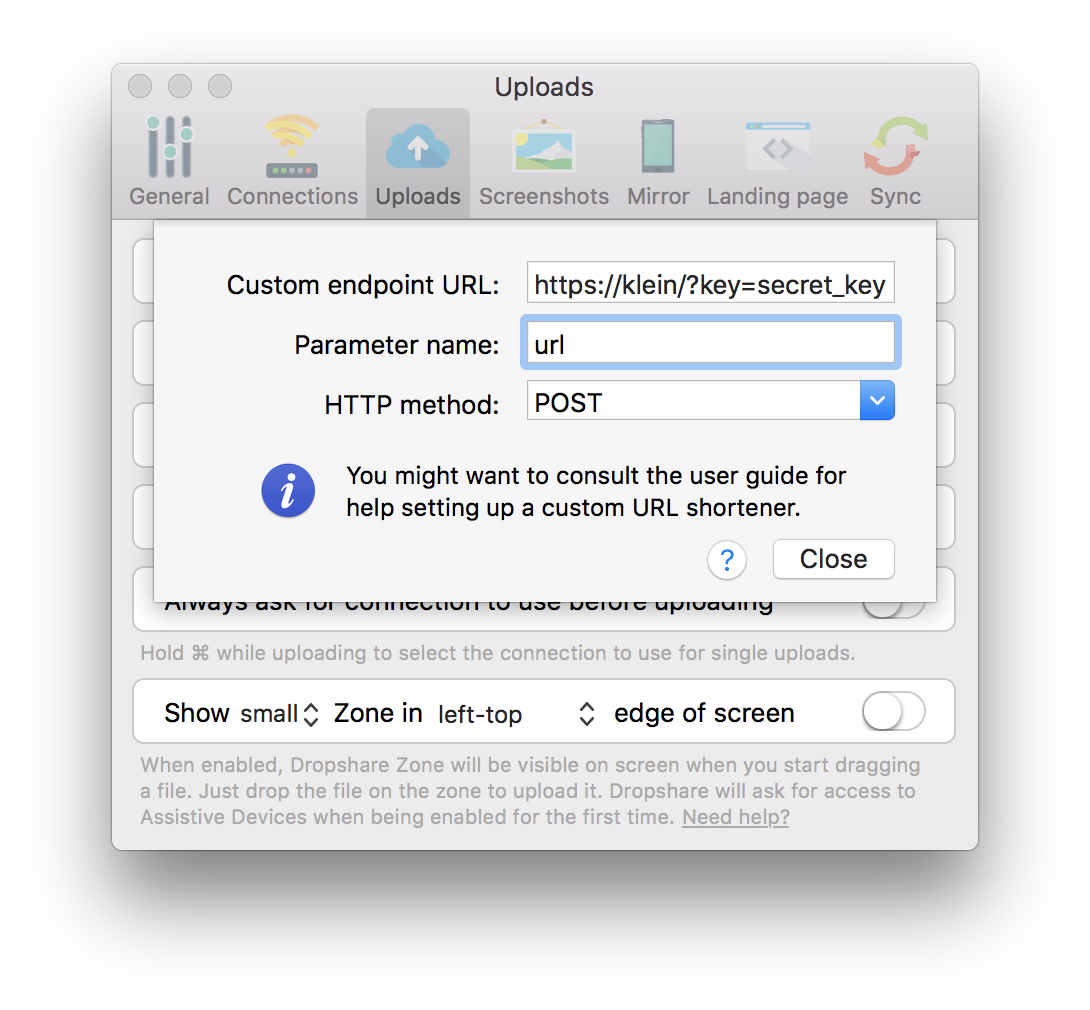
Short URLs

I use my own short URL for files, kmln.sr. This lets me have neat links like https://kmln.sr/qa6. klein is a super easy-to-set-up URL shortener that I wrote and use. The README should provide you with all the necessary documentation. Once that's set up, you can configure Dropshare to use it under the Uploads tab like so:

Useful Resources

• How to set up a DigitalOcean Spaces connection with Dropshare
• An Introduction to DigitalOcean Spaces
• Understanding Nginx HTTP Proxying, Load Balancing, Buffering, and Caching
• How To Secure Nginx with Let's Encrypt on Ubuntu 16.04.
• Object Storage tutorials